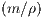
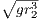 = 20, where m is the mass of the car, ρ is
a damping coefficient to account for friction, and g is the
acceleration due to gravity.
= 20, where m is the mass of the car, ρ is
a damping coefficient to account for friction, and g is the
acceleration due to gravity.
ABSTRACT
This paper examines the design optimization of a Tilt-A-Whirl ride, as an extension of Kautz’s Chaos at the amusement park: Dynamics of the Tilt-A-Whirl [?]. In particular, the task of optimizing passenger experience is analyzed and solved. The objective, the passenger’s enjoyment, is approximated by the standard deviation of each car’s intrinsic angular velocity, found through numerical integration. A Gaussian process surrogate model is used to approximate the system’s time dependent objective, in order to save on computationally intensive evaluations of the true objective function. A hybrid particle swarm algorithm is used to optimize the ride’s design parameters in order to maximize the passenger’s enjoyment. It is shown that a final objective value of over 200% better than the nominal, yielded from the parameters presented in [?], is achievable.
Index Terms— Amusement Ride, Design Optimization, Particle Swarm, Gaussian Process
1.
Following the work of [?], the dynamical model of a Tilta-A-Whirl is revisited. Like many other dynamical systems governed by deterministic equations, the Tilt-A-Whirl is found to exhibit chaotic behavior. In the dynamical model being examined, each of the Tilt-A-Whirl cars are free to pivot about the center of their own circular platform. The platforms move along a hilly circular track that tilts the platforms in all possible directions. While the translation and orientation of the platforms are completely predictable, each car whirls around in an independent and chaotic fashion.
1.1.
1.1.1.
For this paper’s application, there are three design variables which
are taken to be constant at the nominal values presented in
[?], namely: the beam length from the center of the ride to
the center of each platform r1 = 4.3 m, the radial incline
offset of the platform α0 = 0.036 rad, and the parameter
Q0 = 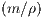
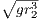 = 20, where m is the mass of the car, ρ is
a damping coefficient to account for friction, and g is the
acceleration due to gravity.
= 20, where m is the mass of the car, ρ is
a damping coefficient to account for friction, and g is the
acceleration due to gravity.
1.1.2.
For the design optimization problem analyzed in this paper, three
parameters are chosen to be manipulable, namely: the extrinsic
angular velocity of the platform ω = 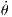 ∈ [0.3142,0.8378] rad∕s,
the length of the radial arm from the center of each platform to the
approximate center of gravity of the car r2 ∈
∈ [0.3142,0.8378] rad∕s,
the length of the radial arm from the center of each platform to the
approximate center of gravity of the car r2 ∈![[0.1,1.5]](TemplateICATT3x.png) m, and
the maximum/minimum incline angle of the beam from
the center of the ride to the platform α1 ∈
m, and
the maximum/minimum incline angle of the beam from
the center of the ride to the platform α1 ∈![[0,0.3]](TemplateICATT4x.png) rad.
The nominal values of the design variables are given as
{ω,r2,α1}0 = {6.5 × (2π∕60) rad∕s,0.8 m,0.058 rad}. Both
the constant parameters and variable design parameters can be
seen within a clearer context in Figure 2. In an object-orientated
manner, a Tilt-A-Whirl car can be programmatically instantiated
with these nominal parameters and bounds, as shown in
Listing 1. The remaining parameters are discussed in latter
sections.
rad.
The nominal values of the design variables are given as
{ω,r2,α1}0 = {6.5 × (2π∕60) rad∕s,0.8 m,0.058 rad}. Both
the constant parameters and variable design parameters can be
seen within a clearer context in Figure 2. In an object-orientated
manner, a Tilt-A-Whirl car can be programmatically instantiated
with these nominal parameters and bounds, as shown in
Listing 1. The remaining parameters are discussed in latter
sections.
From [?], the second order differential equation of motion governing the Tilt-A-Whirl is defined as
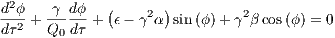 | (1) |
, where the dimensionless parameters are defined as
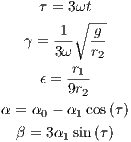 | (2) (3) (4) (5) (6) |
1.3.
Of course, because Equation 1 is rather nonlinear and chaotic, an
analytical closed form solution does not exist. Thus, in order to
observe the behavior of the system over time, it is necessary
to numerically integrate the equation of motion. From a
programmatic approach, one can implement Matlab’s ode45 [?], using the widely popular Runge-Kutta method of fourth and
fifth order. From the object oriented appoach taken in this
paper, this process manifests itself in the form of Listing 3.
2.
It is supposed that the unpredictability of each car’s intrinsic
angular velocity 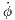 is directly correlated to passenger enjoyment.
Thus the objective measure of design performance is defined as
the standard deviation of each car’s intrinsic angular velocity
σ
is directly correlated to passenger enjoyment.
Thus the objective measure of design performance is defined as
the standard deviation of each car’s intrinsic angular velocity
σ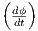 , where
, where  is obtained through numerical integration, as
discussed in Section 1.3.
is obtained through numerical integration, as
discussed in Section 1.3.
2.1.
Herein, the true objective function σ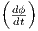 is referred to as a
function of design parameters σ
is referred to as a
function of design parameters σ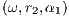 , or less verbosely as σ.
After numerical integration of the system’s dynamics, a large list
of
, or less verbosely as σ.
After numerical integration of the system’s dynamics, a large list
of 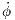 data points are obtained, from which the computation of σ
draws from. However, because the system’s dynamics, described
in Equation 1, are with respect to the non-dimensional parameter
τ, it is necessary to redimensionalize when computing the
standard deviation of the car’s intrinsic angular velocity. The
programmatic transcription of this objective function is seen in
Listing 4.
data points are obtained, from which the computation of σ
draws from. However, because the system’s dynamics, described
in Equation 1, are with respect to the non-dimensional parameter
τ, it is necessary to redimensionalize when computing the
standard deviation of the car’s intrinsic angular velocity. The
programmatic transcription of this objective function is seen in
Listing 4.
Note that only the last two thirds of the 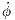 data points are taken
into account. This is done to disregard the start-up of the system,
and only take heed to the terminal dynamics, so as to compute a
purer standard deviation.
data points are taken
into account. This is done to disregard the start-up of the system,
and only take heed to the terminal dynamics, so as to compute a
purer standard deviation.
The nature of the true objective function σ can be seen by keeping α1 and r2 constant, while manipulating ω, as shown in Figure 3. Of course, the evaluation of this objective function is quite computationally expensive, as each evaluation elicits the numerical integration of the system’s equation of motion. It can also be seen that the true objective function is rather noisy, not lending itself well to gradient based optimizers, such as fmincon [?], at all. A conventional optimization algorithm would indeed become trapped within the multiple local extrema that are exhibited.
2.2.
Taking note of the nominal constant parameter values and design parameter bounds described in Section 1.1, the statement of the optimization problem is more formally formulated as
 | (7) |
Because the true objective function σ is so noisy, chaotic, and computationally costly to evaluate, the appropriate course of action is to model the system’s time-dependent behavior with a surrogate model.
2.3.1.
The true objective function is sampled at various design parameter
values using Latin hypercube sampling, with the use of lhsdesign
[?]. Latin hypercube sampling allows for near random sampling of
the design space, to allow for the proper construction of the
surrogate model. Programmatically this sampling is transcribed as
shown in Listing 5.
It is important to note that, initially, the sample values returned by lhsdesign are not scaled to the problem’s parameters; scaling must be done according the scale length of the problem’s bounds. The function shown in Listing 5 returns both the sample design parameter values and the true objective function values at those parameters. The reader is encouraged to consult [?] for a rigorous analysis of Latin hypercube sampling.
2.3.2.
Using the work of Rasmussen [?], a Gaussian process surrogate model is constructed to approximate the computationally expensive true objective function. The Gaussian process library is a machine learning library that addresses the supervised learning problem of mapping inputs to outputs, with previous knowledge of labelled training data. Using the Latin hypercube sampling described in Section 2.3.1, the surrogate model training process is instantiated in Listing 6, from which the Gaussian process hyperparameters are returned.
Using the true objective function samples, the
surrogate model effectively learns the topology of the
design space, through the training occurring during
hyp = minimize(hyp, @gp, -100,@infExact,[],@covSEiso, @likGauss, xs, ys),
in which the Gaussian process hyperparameters are minimized.
Note that, in Listing 6, the hyperparameters and sampling points
are saved, and used later unless the Gaussian process parameters have changed. This allows for significantly faster work-flow when
testing different optimization algorithms.
From the Gaussian process hyperparameters returned from
Listing 6, the surrogate model in Listing 7 acts as a callable
function, herein refereed to as  , that can be inexpensively
evaluated in the optimization process. One major advantage of the
surrogate objective function
, that can be inexpensively
evaluated in the optimization process. One major advantage of the
surrogate objective function  in Listing 7 over the true
objective function σ in Listing 4, is that it is smooth and
is much nicer to optimize, especially with gradient based
methods.
in Listing 7 over the true
objective function σ in Listing 4, is that it is smooth and
is much nicer to optimize, especially with gradient based
methods.
With the Gaussian process surrogate model transcribed in Listing 7, the single varriable design space topologies can be seen with 95% confidence bounds in Figure 5, with 200 Latin hypercube samples. Note the vastly smoother topology in Figure 5 compared that of Figure 3.
With the use of function [X,Y,F] = Surface(self, cvar, np),
the topology of the design space within the neighborhood of the
nominal parameters can be seen in Figure 7. It can be seen that
both 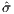 (r2,α1) and
(r2,α1) and 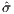 (ω,α1) are fairly nice look, while
(ω,α1) are fairly nice look, while 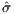 (ω,r2)
seems rather treacherous.
(ω,r2)
seems rather treacherous.
Particle swarm is a population-based stochastic optimization algorithm. It solves an optimization problem by a population of possible solutions, otherwise known as particles, and moving the particles around in the design search space, according to the particles’ positions and velocities. Every particle’s movement is influenced by its best known local solution. However, the particles are also directed toward the best known positions in the design search space among other particles. In effect, this influences the swarm of particles to congregate upon the best solution. This optimization technique was inspired by the social behavior of bird flocking and fish school. The reader is encouraged to consult [?] for more information on this algorithm.
In order to implement this, Matlab’s particleswarm [?] function is used to optimize the surrogate function. This optimization algorithm is made particularly effective when parallelized on multiple CPU cores and augmented with the terminal use of a gradient based optimizer, such as fmincon [?]. Essentially the particle swarm optimization coarsely hones in on the global optimum, at which point a gradient based optimizer pinpoints the solution, assuming the design space is sufficiently convex within the vicinity of the solution.
The particle swarm optimization process can be intuitively
commenced with [x,fval] = TW.Optimize('particle-swarm').
With a Gaussian process surrogate model constructed with 100
samples, an objective standard deviation value of 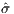 100 = 5.37419
is obtained, as shown with convergence history in Figure 8. With
600 true objective samples, a better objective of
100 = 5.37419
is obtained, as shown with convergence history in Figure 8. With
600 true objective samples, a better objective of 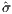 = 6.17409 is
obtained, as seen in Figure 9.
= 6.17409 is
obtained, as seen in Figure 9.
Objective values returned by the optimizer tend to get better
as the resolution of the true objective function sampling
increases, that is the number of samples Ns. However, it has
been found that returns tend to decline as the resolution
becomes very large. This is because, as the resolution of
the surrogate function becomes greater, it exposes more
detail of the true design space. Small details which may have
been disregarded at lower sample values, become apparent,
as shown in Figure 10, giving surrogate objective values
of Ns = {10,100,200,400,600,1000,2000}
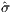 =
{3.5879,4.0953,5.2154,6.2128,6.5701,6.2818,5.5852}.
However, the accuracy of the surrogate model and particle swarm
optimization have been verified, yielding objective values over
200% better than the nominal, for almost all values of Ns. The
Gaussian process surrogate model’s optimal design space
topology can be seen in Figure 12.
=
{3.5879,4.0953,5.2154,6.2128,6.5701,6.2818,5.5852}.
However, the accuracy of the surrogate model and particle swarm
optimization have been verified, yielding objective values over
200% better than the nominal, for almost all values of Ns. The
Gaussian process surrogate model’s optimal design space
topology can be seen in Figure 12.
Through the particle swarm optimization process outlined in
Section 2.4, with Ns = 600, an objective surrogate function
value of 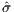 = 6.1741 is obtained with design parameters
{ω*,r2*,α1*} = {0.7703,0.1000,0.2716}. Evaluating the
true objective function σ at these design parameters yields
σ(ω*,r2*,α1*) = 6.6079, thereby further guaranteeing the
accuracy of the Gaussian process surrogate model implemented,
and demonstrating a colossal 312.99% improvement over the
nominal σnom = 1.6. Interestingly, the optimal design parameter
r2* tends to converge to its lower bound.
= 6.1741 is obtained with design parameters
{ω*,r2*,α1*} = {0.7703,0.1000,0.2716}. Evaluating the
true objective function σ at these design parameters yields
σ(ω*,r2*,α1*) = 6.6079, thereby further guaranteeing the
accuracy of the Gaussian process surrogate model implemented,
and demonstrating a colossal 312.99% improvement over the
nominal σnom = 1.6. Interestingly, the optimal design parameter
r2* tends to converge to its lower bound.